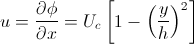Hasil Akhir Aliran Internal Laminar

Inilah hasil simulasi CFDSOF aliran internal laminar yang saya kerjakan, dan bisa dilihat di video yang telah saya upload. Dari gambar terlihat perbedaan tekanan dari bagian yang terdekat dengan dinding pipa sampai aliran yang ada di dalamnya. Selain itu, pada bagian dinding pipa yang mempunya tegangan gesernya sama dengan nol. Pada pembuatan aliran ini, saya membuatnya denga mengatur beberapa wall agar terlihat perbedaan tekanannya. Rumus dari gaya Wall adalah

Nah, dari gambar ini kita juga bisa melihat perhitungan dari gaya wallnya yaitu,

Prosedur Simulasi Aliran Eksternal Laminar

1.Buka Aplikasi CFDSOF, pilih Input-Alokasi Memori-Ya.

2.Pilih Input-Domain, lalu Atur dimensinya ( P,T,L ) dan Jumlah Cell, lalu pakai dan tutup.

3. Pilih Input-Model, pakai dan tutup

4.Pilih Input-Atur Cell- Zona Tipe : W-Wall ; ID : 1

5. Pilih Zona Tipe : Inlet ; ID : 1, ini berguna sebagai saluran masuk fluida

6.Pilih Zona Tipe : Outlet ; ID : 1, ini berguna sebagai saluran keluar fluida

7.Pilih Zona Tipe : W-Wall ; ID : 2 dan lakukan langkah yang sama dengan hanya menukar ID nya mulai dari 3 sampai 6. Membuat wall yang berbeda agar terlihat saat simulasi terlihat perbedaan tekanannya. Lalu tayang, sehingga terlihat hasil akhirnya

8. Pilih Input-KS-Zona tipe : Inlet- Setting- Atur kecepatannya ( U ).

9. Ketik in-kf-dn-vs masukkan sesuai dengan fluida yang akan kita pakai.
10. Pilih Olah-Iterasi, masukkan jumlah iterasinya

11. Pilih Hasil-Kontur-Kecepatan-Velocity Magnitude-Tayang, lalu hasil akhirnya

Terlihat perbedaan tekanan disetiap wallnya

12. Ketik es-es-al-pv-gw lalu akan terlihat hasil gaya wall disetiap wallnya

Video Simulasi Aliran Eksternal Laminar

Video Simulasi Aliran Internal Laminar

Pembahasan Soal 8.20 ( Buku Munson )

Minyak (berat spesifik = 8900 N/m³, viskositas = 0,10 N.s/m²) mengalir melalui sebuah tabung horizontal berdiameter 23mm seperti yang ditunjukkan pada gambar di bawah ini. Sebuah manometer tabung-U digunakan untuk mengukur penurunan tekanan sepanjang tabung. Tentukan kisaran dari nilai h agar alirannya laminer!

Diketahui :

Ditanya  :  h =.....?

Jawab    :  

Untuk aliran laminar, Re kecil sama 2100, dimana massa jenis adalah gamma dibagi grafitasi. Maka, nilai minimum h adalah h = 0 (tidak ada aliran) dan nilai maksimum h adalah untuk Re = 2100. Sehingga,

Untuk fluida viskos yang mengalir,

dengan z₁ = z₂ dan V₁ = V₂ = V. Sehingga,

Penjelasan Teori Soal 8.20 ( Buku Munson )

dE adalah energi total pada sebuah sistem dimana energi potensial dan energi kinetik. 2 energi ini merupakan energi dasar pada alam. Perubahan energi merupakan input dari sebuah system.

W adalah kerja yang dihasilkan oleh gaya. Karena energi digunakan oleh sistem, sistem menghasilkan output  berupa kerja.

Q adalah panas yang dihasilkan oleh sistem. Panas adalah hasil dari output. Hampir tidak ada system yang ideal, sehingga tidak mungkin semua input bisa dijadikan output, oleh karena itu harus ada yang hilang karena interaksi dari sistem itu sendiri.

Persamaan Bernoulli yang di bawah ini,

memiliki satu energi  dan dua kerja. Kerugian nya tidak diikutkan dalam persamaan tersebut, Jika kerugiannya diikut sertakan,Bernoulli akan bekerja pada kondisi real, dan persamaan menjadi,

Dalam persamaan Bernoulli, tidak ada energi yang hilang,namun berubah ke bentuk lain. Persamaan Bernoulli hanya berlaku pada fluida ideal.

z 2 = losses (kerugian) yang terjadi akibat perubahan tekanan statik. Losses ini berupa panas yang didistribusikan ( didisipasi ) kelingkungan sehingga  tidak terdeteksi adanya perubahan temperatur. Pengukuran statik dilakukan  pada tempat yang stagnan sehingga yaitu kinetik. hasil yang didapat bisa dibilang akurat.

Lapisan Batas ( Boundary Layer )

Fluida yang mengalir pada suatu permukaan benda, baik aliran tersebut laminar maupun turbulen, maka partikel-partikel fluida di sekitar permukaan akan bergerak lambat akibat gaya viskos. Patikel-partikel fluida yang berdekatan ke permukaan menempel pada permukaan tersebut dan kecepatannya adalah nol relative terhadap batas. Partikel fluida yang lain berusaha bergerak lambat di atas partikel yang relatif diam tersebut sebagai akibat interaksi antara gerakan fluida yang cepat dan fluida yang lambat. Hal ini merupakan fenomena yang dapat meningkatkan gaya atau tegangan geser. Lapisan fluida yang kecepatannya terpengaruh oleh tegangan geser batas akibat viskositas disebut lapisan batas ( boundary layer ). Daerah yang melingkupi permukaan aliran, dimana tepat di bawah permukaan lapisan batas  terdapat hambatan akibat pengaruh gesekan fluida dan tepat di atas lapisan batas aliran fluida adalah tanpa hambatan.

Ada 2 buah plat yang dipisahkan oleh fluida. Pada plat bawah diam, sedangkan pada plat atasnya bergerak dengan kecepatan U dan terdapat gaya P yang menggerakkan. Plat tersebut mempunyai luas penampang A. Gaya P menghasilkan shear stress. Shear stress dihasilkan oleh viskositas dinamis dikali kecepatan plat dibagi dengan jarak antar plat. Rumus shear stress :

 U/b adalah laju perubahan angular fluida atau disebut juga gradien kecepatan. Karena adanya pesamaan diatas, antara lapisan fluida mempunyai kecepatan yang berbeda beda sebagai fungsi dari y, sehingga masing-masing lapisan fluida bergerak relative satu sama lain. Lapisan yang semakin dekat plat diam maka akan mempunyai kecepatan yang semakin kecil dan membentuk lapisan batas. Jadi, jika shear stressnya semakin besar maka lapisan batasnya juga semakin besar.

 Lapisan batas adalah pendekatan untuk memperkirakan pada daerah viskos ( dalam lapisan batas ) dan non viskos ( luar lapisan batas ). Aliran non viskos adalah aliran yang tegangan geser adalah nol antara fluidanya. Namun, untuk aliran viskos tegangan geser diperhitungkan.

Aliran Dimensional

Simulasi CFD tidak pernah 100 % menyamai kondisi real. Aplikasi fluida dalam kehidupan sehari-hari  sebagai engineer adalah bagaimana kita mendesign sesuatu yang berkarakter, seperti mendesign body mobil . Hal lainnya kita bisa melihat kondisi fluida dalam ruang  bakar, aliran pipa venturi , jika pipa kecil maka tekanan rendah dan kecepatan tinggi, begitu sebaliknya.

Aliran Dimensional

Aliran dimensional adalah suatu metode untuk mereduksi dari parameter satu ke parameter yang lainnya untuk mendapatkan aliran dan geometrinya.

 Satu parameter  yang penting oleh engineer dengan mendapatkan Q (debit), berupa tekanan yang dibutuhkan untuk mendorong aliran fluida.

 Hubungan fungsional secara umum antara variabel yang berlaku untuk sistem pemipaan sejenis. Mengumpulkan variabel tersebut  ke dalam dua kombinasi tak- berdimensi ( produk tak-berdimensi atau kelompok tak-berdimensi ) sehingga,

                                     

Penyederhanaan dari  5  variabel ke 2 variabel. Namun dasar penyederhanaan, berlandaskan pada perhitungan dari dimensi variabel yang terkait. Kita memeriksa dimensi  kedua kelompok , yang secara nyata memperlihatkan bahwa kelompok tersebut adalah produk tak- berdimensi, seperti yang ditunjukkan  dibawah ini.

                               

Kita tidak hanya mengurangi jumlah variabel dari 5 menjadi 2, tetapi kelompok baru tersebut merupakan kombinasi  variabel  tak-berdimensi, yang berarti  bahwa hasil yang ditampilkan

                                                               

akan tidak bergantung pada sistem satuan yang kita pilih, dan analisis seperti inilah yang dinamakan analisi dimensional.

Hukum Reynolds adalah parameter  tak berdimensi yang sangat terkenal dalam ilmu mekanika fluida

Pipa di Dasar Laut

Kestabilan pipa di dasar laut, baik kestabilan dalam arah vertikal maupun arah horizontal, sangat dipengaruhi oleh berat pipeline di dalam air, gaya-gaya lingkungan yang bekerja , serta resistansi tanah di dasar laut. Gaya-gaya lingkungan yang masuk ke dalam analisis kestabilan pipa terdiri dari gaya-gaya hidrodinamika pipa, seperti gaya seret, gaya inersia, dan gaya angkat. Resistansi tanah dasar laut merupakan gaya gesek yang terjadi antara pipa dengan permukaan tanah dasar laut tersebut.

Gambar Diagram Gaya yang Bekerja pada Pipa di Dasar Laut

A.Gaya Horizontal :

   1.Gaya Seret 

      Gaya seret terjadi karena adanya gaya gesekan antara fluida dengan dinding pipa atau yang dikenal sebagai skin friction dan adanya vortex yang terjadi di belakang pipa( form drag ).Terjadi gaya seret sangat dipengaruhi oleh kecepatan aliran.

  2.Gaya Inersia

     Gaya inersia menunjukkan adanya dari masa fluida yang dipindahkan oleh pipa, nilainya dipengaruhi oleh percepatan partikel air.

B.Gaya Vertikal :

   Gaya angkat adalah gaya hidrodinamik dalam arah vertikal, gaya ini terjadi apabila terdapat konsentrasi streamline dalam pipa. Konsentrasi streamline terjadi di atas silinder pipa yang mengakibatkan gaya angkat keatas. Jika terjadi celah sempit antara silinder dan seabed konsentrasi streamline di bawah silinder pipa akan mengakibatkan gaya angkat negatif kearah bawah.

Aliran fluida disekitar silinder 

Aliran disekitar silinder akan menghasilkan resultan gaya pada permukaan silindernya, yang mana terbagi menjadi dua bagian yaitu, pertama gaya yang disebabkan karena adanya tekanan dan kedua gaya yang disebabkan oleh adanya kekasaran pipa, lihat gambar di bawah ini Gaya searah dari resultan gayanya ( karena tekanan ).

Gambar Sketsa Gaya

Adanya vortex shedding akan mengakibatkan adanya komponen gaya transversal  yang umum disebut gaya angkat. Gaya pada silinder akibat gaya gelombang tergantung pada angka Reynolds. Pengaruh lainnya yaitu bentuk benda, kekasaran, turbulensi, dan gaya gesek akan menyebabkan perubahan aliran. Bagaimana pun adanya pengecualian yaitu pada angka Reynolds rendah ( Re<<40 ), dimana umumnya disebut aliran akan mengalami vortex shedding. Sebagai konsekuensi dari phenomena vortex shedding, distribusi tekanan disekitar silinder akan mengalami perubahan yang periodik di dalam prosesnya, sehingga menimbulkan gaya yang berperiodik  pada silindernya. Distribusi tekanan total didapatkan dengan mengintegrasikan tersebut pada permukaan silinder.

Contoh Soal : Kekuatan Maksimum Vortex

Apabila  air mengalir keluar dari sebuah tangki melalui lubang bukaan di dasarnya, sebuah vorteks dapat terbentuk dengan profil permukaan melengkung seperti yang ditunjukkan pada gambar P6.45. Asumsikan bahwa distribusi  kecepatan di dalam vorteks sama dengan sebuah vorteks bebas. Pada saat yang  bersamaan dengan air yang keluar  melalui titik A, diinginkan pula untuk mengalirkan dalam jumlah kecil air keluar melalui pipa B. Jika kapasitas melalui A meningkat kekuatan vorteks juga meningkat sebagaimana ditunjukkan oleh sirkulasinya. Tentukan kekuatan maksimum yang dapat dimiliki vorteks  sedemikian hingga tidak ada udara yang terhisap ke dalam di titik B. Nyatakan jawaban dalam besaran sirkulasi. Asumsikan bahwa ketinggian  fluida di tangki pada jarak yang cukup jauh dari lubang bukaan di A tetap konstan dan efek viskos dapat diabaikan.

Jawab :
Karena vorteks bebas merupakan medan aliran irasional, maka persamaan Bernoulli berikut

dapat dituliskan untuk titik apa saja dalam vorteks tersebut. Jika titik-titik yang dipilih berada di permukaan bebas, dimana  P1=P2=0, maka :

di mana ketinggian permukaan bebas, z_s , diukur relatif terhadap datum yang melalui permukaan atas.

Kecepatannya diberikan oleh persamaan

Kita mengetahui bahwa V₁ = v_θ ≈ 0. Sehingga,

Udara akan dihisap ke dalam pipa saat z_{s =  -1 ft untuk r = 2 ft. Sehingga,}

Dengan demikian,

Contoh Soal : Menentukan Potensial Kecepatan

Diketahui suatu distribusi kecepatan pada aliran dua dimensi dari sebuah fluida viskos di antara dua plat lebar yang paralel membentuk fungsi parabolik, dengan fungsi

dimana v = 0. Tentukan, jika ada,stream function dan potensial kecepatannya !

 Jawab :

Untuk menentukan stream function,

kita dapat mengintegralkan persamaan di atas terhadap variabel "y". Sehingga,

Karena , ψ bukan merupakan fungsi dari x. Maka,

dimana C adalah sebuah konstanta bebas.

Untuk menentukan potensial kecepatan,

kita dapat mengintegralkan persamaan di atas terhadap variabel "x". Sehingga,

Namun karena, 

dan persamaan ini tidak dapat dipenuhi oleh semua nilai x dan y, maka tidak ada potensial kecepatan yang dapat mendeskripsikan aliran ini ( aliran bersifat irasional ).